蜡块实验：如何在平面直角坐标系中研究物体的匀速直线运动

物理学习中的物体运动探究既有趣又充满挑战。比如，蜡块的运动研究，其中蕴含着丰富的知识，既吸引人探究，又可能让人感到迷茫。这正是我们今天要讨论的重点和亮点。

蜡块实验过程

实验中，蜡块在玻璃管中的运动颇有趣味。我们取一根红蜡圆柱体A，置于装满清水的玻璃管中，该管约长一米，并且一端是封闭的。将玻璃管倒过来后，蜡块便沿着管子匀速向上移动。接着，我们将玻璃管沿着黑板水平方向慢慢移动，此时蜡块同时向上和向右移动。这样的实验在普通实验室或教室中都能进行。我们能够清楚地观察到蜡块运动轨迹的变化。通过两个方向的匀速运动，蜡块形成了向上的右方运动，这让我们对运动的合成有了直观的理解。

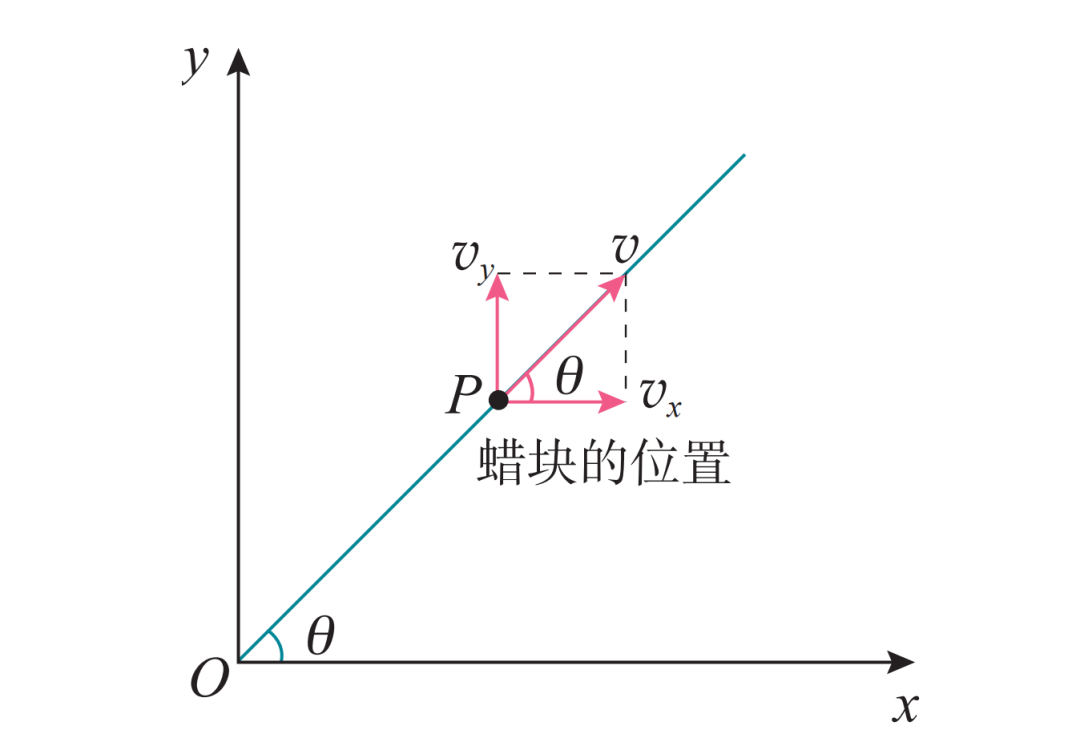
观察蜡块在平面直角坐标系中的移动路径，发现其特点鲜明。以蜡块起始位置作为坐标原点，将向右的水平方向和向上的垂直方向分别标记为x轴和y轴。蜡块在x轴方向上的运动速度等同于玻璃管的移动速度，而在y轴方向上的速度则由其自身上升引起。通过解析相关公式，我们可以确认蜡块的运动轨迹是一条穿过原点的直线，这一发现为探索复杂运动规律提供了新的思路。

速度关系探究

用v、vx、vy来描述蜡块的速度关系非常直观。借助勾股定理，我们能明确它们之间的速度联系。当关注速度方向时，速度矢量v与x轴正向形成的角度θ的正切值同样可以确定。在现实应用中，比如分析物体在空中的斜抛运动，这样的速度关系分析就很有帮助。在工程领域，若需确定物体在垂直方向受力时的速度大小和方向，这样的思考方式同样极为实用。

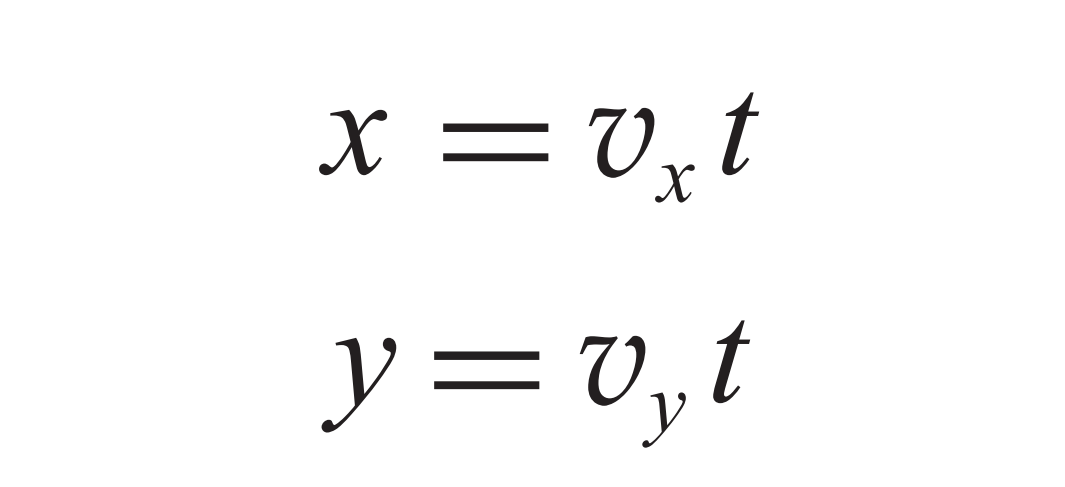
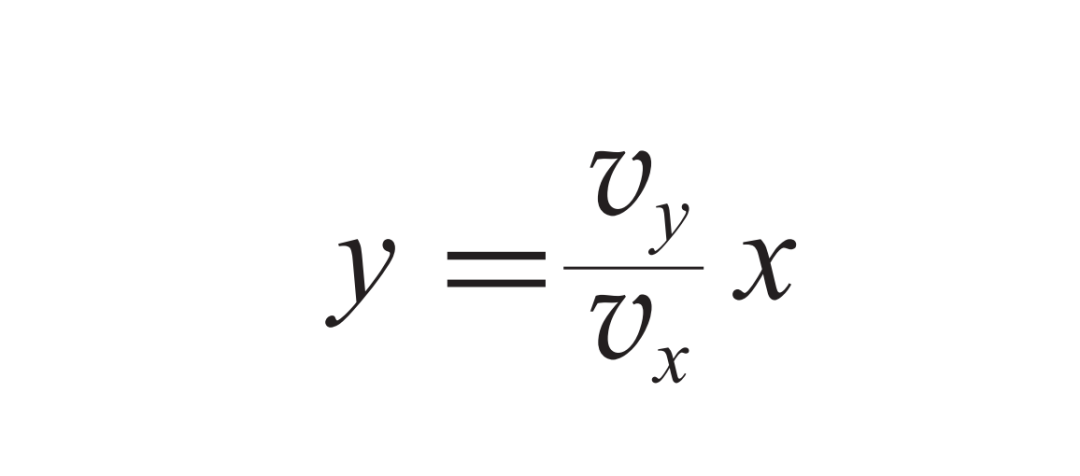
蜡块运动的速度问题与矢量运算有关，这要求我们精确理解矢量的叠加法则。实验中观察到的速度叠加，在理论上是可以通过公式精确描述的。以一艘船为例，它在风和水流的双重作用下前进，其真实速度就可以依据这种方法来分析，这对船员来说，能更有效地规划航线，避免潜在的风险。

最短时间问题相关

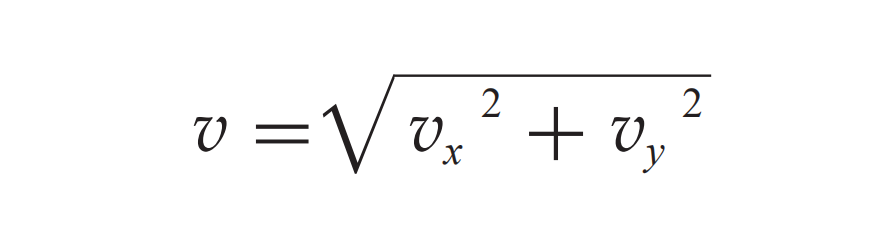
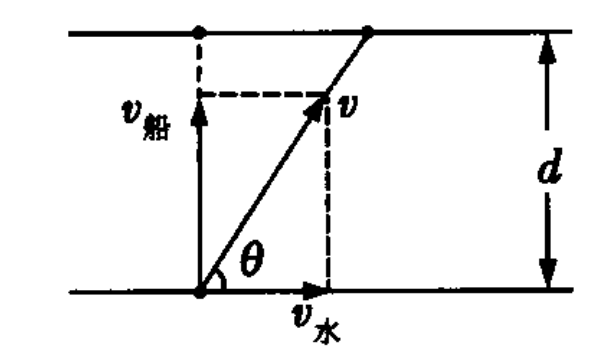
小船横渡河流是蜡块运动理论的一个实际应用。在渡河过程中，小船至少存在两种运动：一是随水流移动，二是相对于静止水面的移动。以岸边为参照物来分析这两种运动的合成，情况会变得相当复杂。若想渡河用时最短，应确保船头与河岸垂直。在此条件下，渡河所需时间t等于距离d除以船速v船，渡河的位移x等于距离d除以正弦值θ，而位移的方向则由正切值θ等于船速v船除以水流速度v水确定。这一结论，通过水流速度和船头方向的考虑，能够精确计算出渡河所需的最短时间。

在真实的渡河情境中，小船的操控很大程度上依赖于这一理论。比如，在一次户外探险中，队员们需横渡一条不算宽的河流，他们必须计算船头朝向以节省时间。再比如，在战争年代，军队要迅速渡过江河抵达对岸，这种理论能帮助士兵高效地操控船只，迅速完成渡河任务。

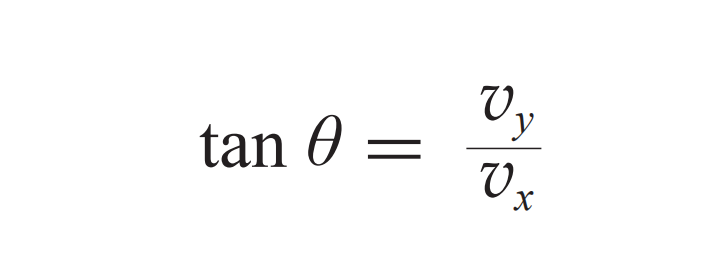
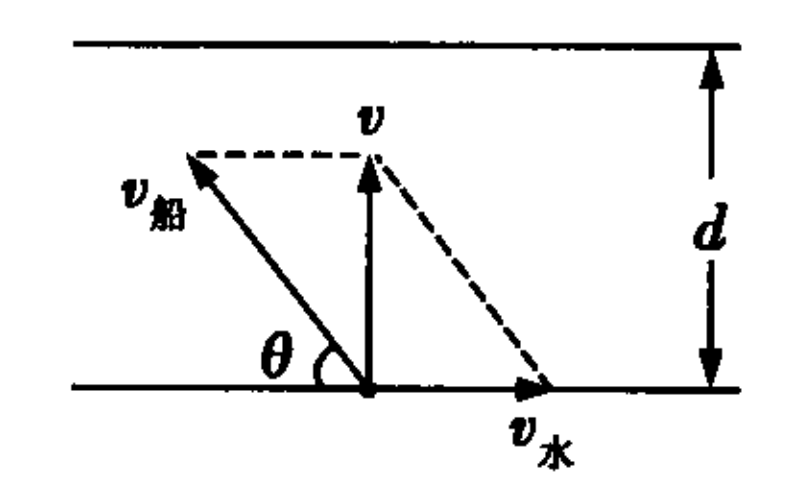
最短渡河位移情况一

研究最短渡河距离的第一种情形，船的航向与河水的流向夹角需满足余弦值等于水流速度与船速之比。在这种情况下，可以精确地算出最短的渡河距离。这在水利工程中的船舶运输尤为关键。例如，在运输建设大坝所需材料时，若能依据这一原理确定船的航向角度，就能有效节约时间和资源，提高工程进度。

这种情况主要是指水位变化不大的河流，或者是人工建造的河流。比如，在工厂附近用来运输货物的较短的人工河流，船只需要根据水流和自身的速度来调整航向，以确保在运输过程中移动距离最短，这样可以减少成本，提升效率。

若河流流速超过船速，这表明河水流速较快，难以驾驭。此时，不论船头朝向何方，都无法垂直于河岸横渡。我们依据水流速度与船在静水中的速度之比，绘制矢量图以确定最佳航向。观察现实生活，若在一条急流的山间河中试图渡河，便可能遇到这种情况。以水流速度的矢量端点为圆心，船在静水中的速度为半径画圆，从起点向圆弧画切线，以此确定船的航向。船头与河岸形成的夹角θ满足cosθ等于船速与水速之比，此法有助于船只以最短距离成功过河。